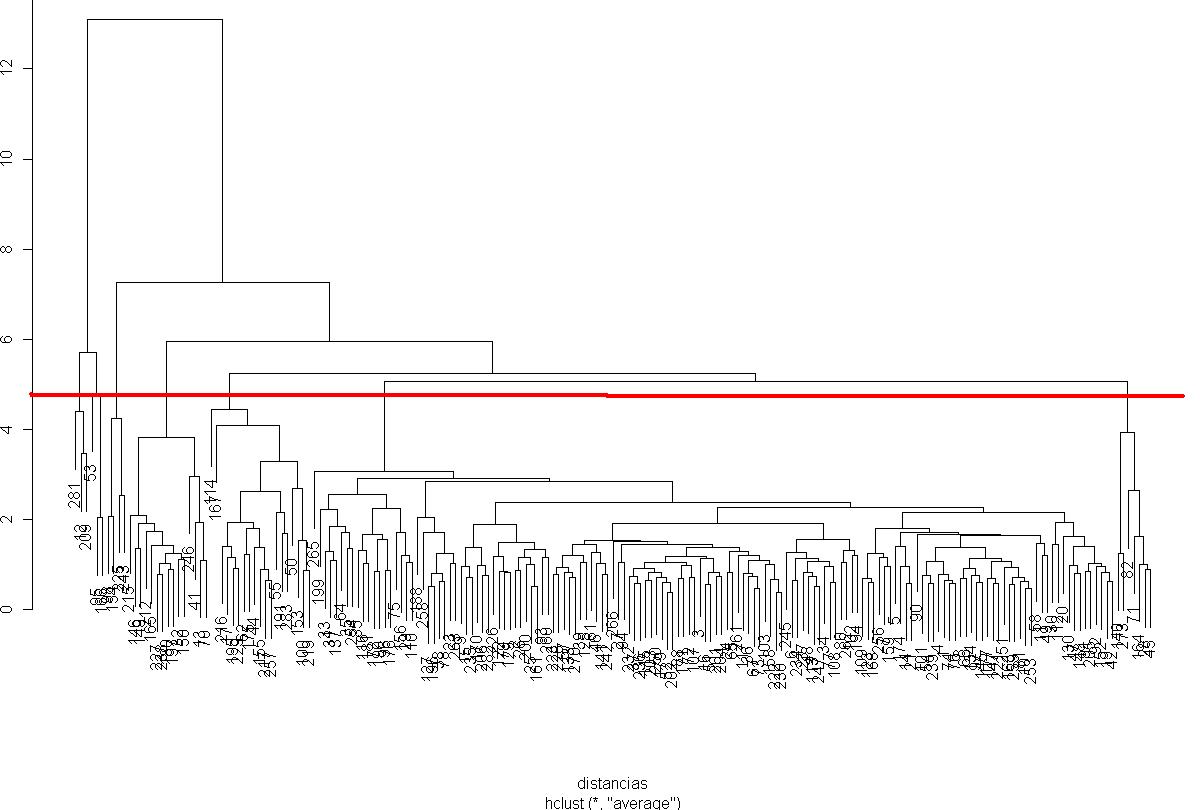
Trucos Excel. Gráficos dot plot, representando un ranking gráficamente
Los gráficos de puntos son muy prácticos para representar de una forma visual rankings (por ejemplo). En Excel su realización no es inmediata como con otras herramientas (R por ejemplo). Para ilustrar el ejemplo se van a presentar los 20 primeros puestos de la lista TIOBE de mayo de 2012 (la entrada estaba en la nevera). Entramos en la lista y sin más copiamos y pegamos los datos de tabla HTML a tabla Excel: