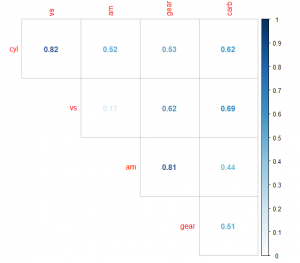
Gráfico de correlaciones entre factores. Gráfico de la V de Cramer
Un gráfico muy habitual a la hora de construir modelos de riesgo para el cálculo de tarifas es el gráfico de correlaciones de la V de Cramer que nos sirve para medir la correlación entre factores, entre variables cuantitativas hace muchos años ya escribí sobre el tema. Hoy os traigo la creación de un corrplot con R aplicado a la V de Cramer y además os descubro una función muy elegante para realizar este análisis de correlaciones entre factores, esta función está sacada de stackoverflow (como no) y añado un análisis gráfico que nos permite conocer algunas opciones de corrplot.
library(vcd)
library(corrplot)
library(tidyverse)
data(mtcars)
#Partimos de una matriz vacía con las dimensiones apropiadas
empty_m <- matrix(ncol = length(correlaciones),
nrow = length(correlaciones),
dimnames = list(names(correlaciones),
names(correlaciones)))
#Calculamos el estadístico y vamos rellenando la matriz
calculate_cramer <- function(m, df) {
for (r in seq(nrow(m))){
for (c in seq(ncol(m))){
m[[r, c]] <- assocstats(table(df[[r]], df[[c]]))$cramer
}
}
return(m)
}
Lo que hace la brillante función es, partiendo de una matriz cuadrada con los factores, ir rellenando con el correspondiente cálculo de la V de Cramer. El resultado final será igual que una matriz de correlaciones por lo que podremos realizar el gráfico.
predictoras <- c("cyl","vs","am","gear","carb")
correlaciones <- select(mtcars,predictoras)
cor_matrix <- calculate_cramer(empty_m ,correlaciones)
#Ya podemos graficarlo
corrplot(cor_matrix, method="number", is.corr=F,type="upper", diag=F, cl.lim=c(0,1))
remove(correlaciones)
El resultado:
Aspectos interesantes con la función corrplot, con method = “number” sale el valor, no me gustan las bolas, aunque podéis probar con pie, mejor poned is.corr = F con type=“upper” sale la parte superior de la matriz, quitamos la diagonal que es 1 con diag=F y la V de Cramer es un valor que va entre 0 y 1 con cl.lim establecemos los límites de la leyenda en el gráfico de correlaciones. A partir de aquí cada uno que establezca un umbral para determinar que dos factores están correlados, yo por ejemplo lo establezco en 0.33, saludos.