En la regresión logística ¿el sobremuestreo es lo mismo que asignar pesos a las observaciones?

Hoy vamos a volver sobre el tema del sobremuestreo. Respondemos a un lector, Roberto, que hace mucho tiempo planteó una duda al respecto. La duda se puede resumir: En un modelo logístico, ¿equivale entrenar un modelo con las observaciones sobremuestreadas a entrenar el modelo poniendo un peso a cada observación? Esta cuestión nunca me la había planteado. Siempre había realizado un sobremuestreo de las observaciones adecuando la población de casos negativos a la población de casos positivos. Si estás habituado a trabajar con Enterprise Miner de SAS es habitual asignar pesos a las observaciones para realizar el proceso de sobremuestreo. ¿Obtendremos distintos resultados?

Vamos a estudiar un ejemplo con SAS y analizar que está pasando:

*REGRESION LOGISTICA PERFECTA;

data logistica;

do i=1 to 100000;

  x=rannor(8);

  y=rannor(2);

  prob=1/(1+exp(-(-5.5+2.55*x-1.2*y)));

  z=ranbin(8,1,prob);

  output;

end;

drop i;

run;

title "Logistica con un 5% aprox de casos positivos";

proc freq data=logistica;

tables z;

quit;

Tenemos un conjunto de datos SAS con 100000 observaciones aleatorias y dos variables independientes (x e y) con distribución normal y creamos una variable dependiente z que toma valores 0 o 1 en función de la probabilidad de un modelo logístico. Es decir, podemos modelizar una regresión logística perfecta con parámetros Z=5.5 – 2.55x + 1.2y Esta distribución nos ofrece aproximadamente un 5% de casos positivos. A ser un modelo logístico perfecto si realizamos la regresión lineal sobre los datos obtendremos:

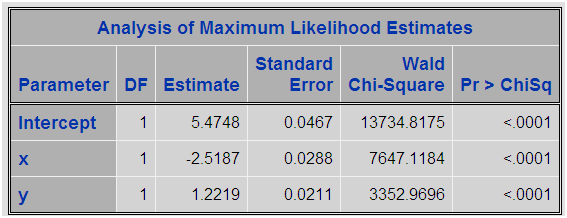
title "Ajuste de logistica perfecto";

proc logistic data=logistica;

model z=x y;

quit;

Un modelo casi perfecto. Ahora vamos a realizar un proceso de sobremuestreo y analizar los parámetros:

*MUESTRA ALEATORIA CON REEMPLAZAMIENTO;

PROC SURVEYSELECT DATA=logistica (where=(z=1))

 OUT=unos METHOD=URS N=50000 outhits ;

RUN;

*MUESTRA ALEATORIA SIMPLE;

PROC SURVEYSELECT DATA=logistica (where=(z=0))

 OUT=ceros METHOD=SRS N=50000;

RUN;

data logistica2;

set unos (drop=numberhits) ceros;

run;

title "Ajuste a logistica con sobremuestreo";

proc logistic;

model z=x y;

quit;

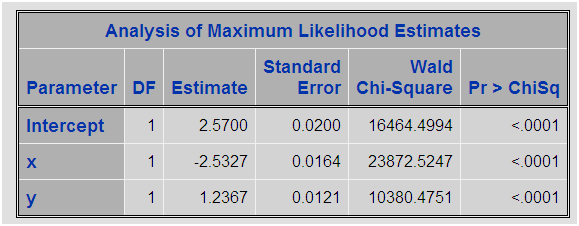
Con el PROC SURVEYSELECT en un primer paso realizamos un muestreo con reemplazamiento para los casos positivos, posteriormente realizamos un muestreo aleatorio simple para los casos sin evento. Unimos ambas tablas y realizamos el PROC LOGISTIC para la nueva tabla con proporción 50% de unos y 50% de ceros:

Sólo ha variado el término independiente que se ha reducido a la mitad (más o menos). [A ver si alguien puede contar porqué se está produciendo este hecho]. Pero lo que más nos interesa es saber qué sucede si en vez de realizar el sobremuestreo asignamos pesos a las observaciones. ¡Ojo! No vamos a crear una variable offset en el modelo, vamos a asignar un peso a cada registro de la tabla, eso es un tema interesante que necesitaría otra entrada en el blog. El proceso de creación de esta variable peso es muy sencillo:

*AHORA VAMOS A ASIGNAR PESOS A LAS OBSERVACIONES;

proc sql noprint;

select sum(z)/count(*) into: pct

from logistica;

quit;

data logistica3;

set logistica;

if z=0 then peso=0.5/(1-&pct.);

else peso=0.5/&pct.;

run;

proc means data=logistica3 sum nway;

class Z;

var peso;

run;

title "Ajuste a logistica con pesos";

proc logistic data=logistica3;

model z=x y;

weight peso;

quit;

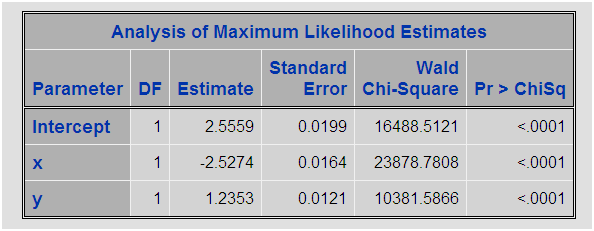
El peso consiste en dividir el porcentaje que deseamos entre el porcentaje real, así de sencillo, al final la suma del peso de las observaciones será igual al total de las observaciones. En el PROC LOGISTIC añadimos la sentencia WEIGHT para indicar que variable contiene el peso. El resultado de este modelo es:

Prácticamente el mismo modelo que hemos obtenido con el proceso de sobremuestreo. Así que estamos en disposición de asegurar que asignar pesos a las observaciones y emplear estos pesos para realizar los modelos de regresión logística equivale a realizar el sobremuestreo. Reiterando, no es lo mismo que emplear una variable offset en el modelo. Con esto espero que antes de realizar complejos procesos de muestreo para detectar patrones con modelos de regresión logística asignéis pesos a registros.

Ahora queda extrapolar estas conclusiones a otros modelos. Saludos.