Cuidado con el p-valor. Depende del tamaño de la muestra

El otro martes, Teresa mi profesora de la Facultad de Estudios Estadísticos, dijo una frase que me dejó helado.“Ojo con el p-valor porque depende del tamaño muestral” Estábamos estudiando regresión logística y test de independencia. Ahora que uno mismo vuelve a estudiar que es lo que hay detrás de la salida de los programas estadísticos se plantea muchas dudas. Por definición el p-valor depende del tamaño muestral y es una medida que la tomamos como un axioma para todo: El p-valor nunca miente hasta que tenemos mucha exposición. Voy a utilizar un ejemplo que vi en clase con Teresa ligeramente retocado (no creo que se enfade, no creo ni que lea esto). Trabajo con SAS porque estoy más acostumbrado a la salida que ofrece. Se trata de realizar un test de independencia para una tabla 2×2. La H0 o hipótesis nula es que existe independencia entre el factor de nuestro estudio y la variable dependiente en nuestro caso H0 es no hay relación entre la utilización de un pesticida y la presencia de una enfermedad frente a H1 hay relación entre la utilización del pesticida y la presencia de la enfermedad. Simulamos los datos con SAS:

data datos;
do i=1 to 85;
pesticida = 0; enfermedad = 0; output; end;
do i = 1 to 15;
pesticida = 0; enfermedad = 1; output; end;

do i = 1 to 168;
pesticida = 1; enfermedad = 0; output; end;

do i = 1 to 31;
pesticida = 1; enfermedad = 1; output; end;
run;

proc freq; tables pesticida*enfermedad; quit;

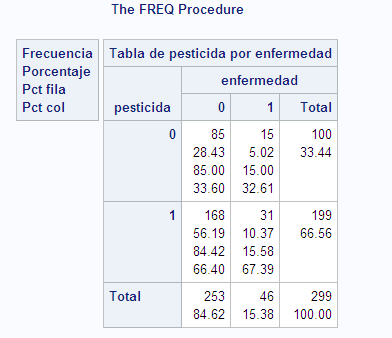
Si realizamos un modelo de regresión logística sobre esta tabla 2×2 y vemos la salida correspondiente al test de Wald:

proc logistic data=datos;
class pesticida;
model enfermedad = pesticida;
quit;

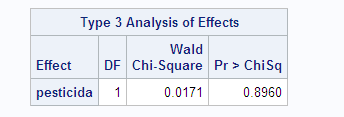
Como el p-valor es mayor de 0,05 no rechazamos la H0. No hay relación entre estar expuesto al pesticida y la enfermedad. Estamos de acuerdo todos. Con esa cantidad de individuos hay independencia. Pero, ¿con las mismas proporciones y muchos más individuos que pasa? Si aumentamos el número de individuos, ¿disminuye el p-valor? Un proceso iterativo y sobre cada iteración volvemos a recalcular el p-valor:

ods select none;
data datos2; run;
data wald; run;

*MACRO CON 250 ITERACIONES;
%macro doit();
%do i=1 %to 250;
data datos2;
set datos2 datos;
run;

*PARA CADA ITERACION NOS QUEDAMOS CON EL TEST DE WALD;
ods output Type3=wald_aux;
proc logistic data=datos2;
class pesticida;
model enfermedad = pesticida;
quit;
*UNIMOS TODAS LAS ITERACIONES;
data wald_aux;
set wald_aux;
ejecucion = &i.;

data wald;
set wald wald_aux;
run;

%end;
%mend;

%doit;

data wald;
set wald;
if _n_=1 then delete;
run;

*GRAFICAMOS EL PROCESO;
ods select all;
proc sgplot data=wald;
series x=ejecucion y=probchisq/;
yaxis max=1 min=0;
refline 0.05;
run;quit;

Como resultado obtenemos…

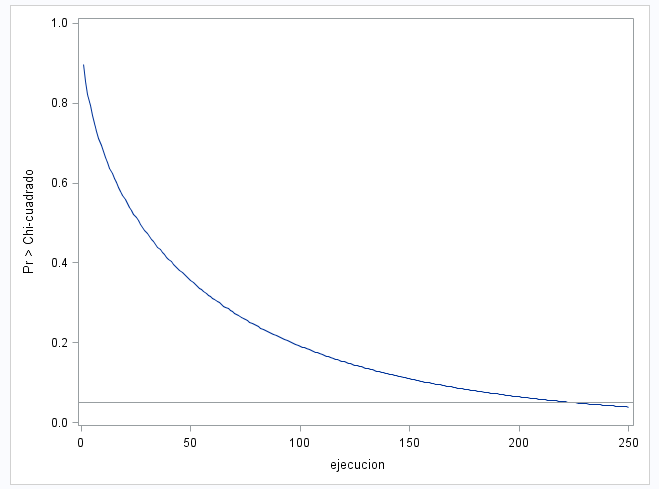
Al final terminamos por no rechazar la H0. Menos mal que nos queda el odds ratio y los intervalos de confianza, pero de eso hablaremos otro día. Saludos.